计算教学可以如此美妙

——“除数是两位数的笔算除法”教学实录及评析

执教  湖南省长沙市开福区清水塘二小        刘友华

评析  湖南省长沙市开福区教育科研培训中心  易虹辉

【背景介绍】   

2010年11月，刘友华老师应邀参加“湖南省30所名优学校送课到革命老区平江县”的大型支教活动。执教内容是当地老师指定的人教版数学教材四年级上册84页例2“除数是两位数的笔算除法（除数接近整十数）”。

【教学实录】

一、创设现实情境，让学生感受估算的作用

师：听说咱们平江的香干特别好吃，又香又辣，是吗？

生：（坚定的说）是！

师：昨天我就到超市选购了一番。我给我们学校的数学老师每人各买了一包，一共21包，需要168元。（板书21和168。）我在付钱给营业员时，突然想到了一个数学问题，猜猜是什么？

生：每包要多少钱？

师：遇到知音了！谢谢你！（我拥抱一下这个学生，并建议大家为他鼓掌，这可是第一个举手发言的孩子。）

师：请大家帮我想一想：每包的价钱超过10元吗？

生：没有。

师：你怎么知道没有超过？

生：因为，如果是10元一包，那么就要200多块钱了。

（大家表示赞同并鼓掌，不需要我提醒了。）

师：那每包超过5元吗？

生：超过了。因为每包5元，21就是100多元，比168少，所以没超过。

师：开始说超过，现在又说没超过，到底超没超过？

生：超过了，因为21乘5等于105，而你付了168元，说明，不止5元一包，所以超过了。

（大家鼓掌。）

师：看来这香干的价格是5到10元之间，这个价格比较合理。

【点评：课始，教师根据送课的现实背景巧妙地创设“买特产”的话题，很快拉近了自己和这群陌生孩子的距离。看似随意的聊天，实则学生不知不觉就投入到了今天的学习任务之中，而简约的估算过程也为下面的“试商”打好了基础。】

二、充分展现学生计算的方法，试图说出算理

1、初次探究，交流算法。

（课件出示香干图及问题：）

师：我现在想知道每包香干的价格具体是多少，该怎么办？

生：计算。

师：对，要算一算。请把你的想法、算法写在本子上，可以写口算的过程，也可以用竖式计算，还可以画图。不管你用什么方法，第一要能算出结果，第二要让别人看明白，看看你能找到几种算法？

（生独立思考，师指名一些同学将方法板书在黑板上：

方法一：168≈160                    方法二：

        21≈20                            

        160÷20=8   

        168÷21=8

方法三：                            方法四：

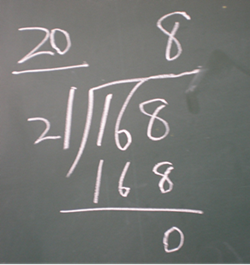
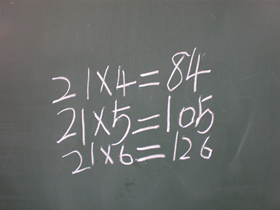
方法五：

师：有这么多方法，你们看懂了吗？说说你看懂的方法。

（生开始不敢说，等待片刻后开始有人举手。）

生1：我看懂了第五种方法，他是把168，以21为一段，一共分成了8段。（学生表示赞同。师引导大家数一数，发现确是8段。）

生2：我看懂了第三种方法，他是用竖式计算的。

师：（指着竖式中的个位）为什么这个8写在这个位置？

生2：因为是表示8元钱。

师：如果写在这里呢？（将8写在168的6上面。）

生2：不行，那样就表示80元了。

师：哦，我的香干要80元一包吗？

生：（笑了）不要。

（师生一起商量，把竖式修改完善。师故意将竖式中21乘8的结果错写成160 ，引起学生反对，从而明确正确的写法。）

师：最后相减等于0说明了什么？
   生：没有余数，说明商8对了。

生3：我有点看懂了第一种方法，（168≈160   21≈20  160÷20=8   168÷21=8）他是把168看成160，把21看成20。160除以20等于8 ，168除以21等于8。

（生有的点头，有很多没反应。）

师：我看有不少同学没反应，谁来说说，你哪里不明白？

生4：160除以20等于8没错，但是你怎么就能说168除以21也等于8呢？是猜的吧？

生：（板书的那位同学）我是将他们都看成整数，这样就商8 ，然后把168除以21也商8，用21乘8发现正好是168。所以就能确定168除以21等于8了。

（生纷纷点头。）

生5：我看懂了第二种方法。他先画了16捆小棒，又画了8根小棒。（见图一）

图一

师：完了？这个方法算出168除以21的答案了吗？

生5：没有。

师：没有表达完，咱们只能看懂一部分。谁能把这个图画完？

生5：可以把21根圈在一起，要圈就要打开一捆。（一时找不到21根在哪里，打开一包后还是不知怎么办。）

生6：不要打开了。把这8根移过来一下就可以了。（说着自己上台把8根移到16捆的下面，然后将21根圈起来。如图二。）

图二  

师：感谢这位同学的精彩发言。（老师给了他一个热情的拥抱，孩子高兴地回到了座位。）

生7：方法四我不懂，为什么写这三个算式呢？（指着21×4=84；21×5=105；21×6=126。）

师：是呀，这是谁的方法？

生8：（板书的学生回应）我是先算21乘以5等于105，发现不行，所以就乘6等于126。

师：等于126就行了？

生8：还是不行……

（师用期待的眼神望着她。）

生8：我没写完。

师：哦，没写完，那怎么办？

生：（齐喊）上去写完整呀！

（在大家掌声鼓励下，生8在“21×6=126”后面写上“21×8=168”，回到了座位。）

师：你怎么不写21×7呢？

生8：因为21×7也不行。

师：不行就不写了？

生8：是的，不行我就……跳过去了，直接乘8。

（全场自发鼓掌。）

师：这个“跳”字用得好！你写的几个算式就是你的试商过程，很有价值，当试的商小了时，咱们可以加1再试，有时还可以跳一跳来试，这样更快。只要我们坚持不懈，总会得到正确的商。再次表扬这位同学和我们分享她的想法。

（学生看到这个开始做错了的同学得到老师的认可，放得更开了，举手的人也更多，发言的声音更大了！）

师：（指着黑板上的几个算式）请大家再看看她的试商过程，开始咱们先估算了每包香干的价格是5到10元之间，那么还需要用4试吗？

生：不需要。直接从6开始试就可以了。

师：这样咱们就只要试几次就可以了？（生齐答：3次！）如果跳一跳，试几次就行了？（生齐答：2次！）这样计算就会更——（生答：快一些！）

师：我发现下面有同学第一次就试8，一试就中，很厉害。是哪些同学？（有四五个举手。）谁能说说你是怎么想的吗？

生：我是看个位，只有1乘8才得8，所以就直接商8。

师：也就是说根据个位来判断，对吗？这个方法真好。(师竖起大拇指。)

师：在这些方法中你们最喜欢哪一种？

生：喜欢第3种。（指竖式。）

师：竖式是最简洁的一种方法。其他几种方法也都体现了168除以21的计算过程，竖式只是把这些过程简洁地记录下来，我们可以根据情况选择自己喜欢的方法。

（师板书168÷21的结果，并写上单位。）

【点评：学生的精彩源于教师的放手。除法计算本来是一个较为枯燥的内容，可由于教师将思考与表达的空间完全给了学生，因此课堂呈现出了丰富多样的思维，学生这些丰富的算法为课堂交流提供了宝贵资源。接着，教师又引导学生交流算法，孩子们互相理解、质疑、解释、回应，交流使每个孩子在此过程中都能获得新的认识，甚至那个本不太会算的孩子也受到了启发，想到可以“跳一跳”来求商。这是一个多么生动、多么真实、多么自由的学习过程！】

2、再次尝试，选择算法、掌握试商。

师：现在我知道每包香干的价格是8元钱了。想想也不便宜啊！营业员听到了我的话说：现在买这种最实惠了，因为这种有促销活动。

（课件出示：买三包送一包。）

师：我可以送几包呢？

生：送7包。

师：7是怎么得到的？

生：用21除以3得到7。

生：不对，应该是送9包。因为7包还可以送2包。

师：到底是送7包，还是9包？

生：我觉得是7包，因为只说买3包送1包，没说送的还可以再送。

生：是的，老板不会再送的，那样就会亏本的。

师：那我花168元钱一共买到多少包香干了呢？

生：28包。用21加7就是28包了。

（课件出示问题：实际每包多少钱呢？引导学生列出算式：168÷28=？）

师：请把你的方法写下来，看谁算得又快又准！

（教师巡视，指名板书。学生的方法仍然很多样，如下图。）

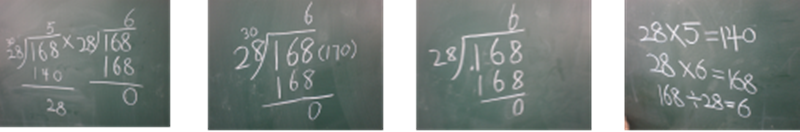
方法一                方法二              方法三               方法四

师：谁来讲讲这些方法？

生：第一种方法是把28看作30，先试5，发现小了，再改试6。

（教师根据学生回答规范书写竖式，重点和学生商量如何调商。）

师：（指着第二种方法）这种方法谁看懂了？

生：他是把28看成30来试商，把168看成170，然后就试6。

师：为什么他就直接试6呢？按说应该是试5呀？

生：是呀！

生：肯定是他早知道商6了。

师：到底是怎样的呢？我们请这位同学说说看。

生：我是这样想的：用170除以30，商5还余20多，因为我把除数看大了，想想商可能会小，所以就试6， 6乘28 正好就是168，不多也不少。

（大家自发地鼓掌。）

师：这个同学不仅把除数看成整十数，还把被除数看成整十数，这样试商就更加简便了。像这样，把新知识转化成旧知识解决问题，是我们数学中常用的方法。（板书：新   旧）

生：第三种方法是直接商6。

师：这个同学很厉害，一试就中。还有谁一试就中的？

（有7、8个举手。）

师：请一个同学说说你的方法。

生：我是这样想的：168的个位是8，1乘28的个位也是8，但商1肯定是不对的；还有6乘8的个位也是8，所以我就直接商6了。

师：这就是我们前面有个同学用过的“个位判断法”，有时它又快又准。

生：第四种方法是从5试起，看看谁乘28等于168。

师：这也就是：做除法，想——（学答：乘法！）

师：现在我们知道了实际每包香干的价格是6元钱。价格还算实惠。我刚才在看大家计算时，发现有个同学算出的结果是16。谁能说说，16为什么错了？

生：16肯定错了。

生：如果是16那么肯定不止要付168元了，最少要200多元。

生：我们前面估计过每包不超过10元的，后来商场还促销，所以肯定不会超过10元的。16肯定错了。

师：大家说得很好。在我们计算时，先估计大约的结果，可以避免不应该的错误。

【点评：再次尝试，讲台和黑板仍然是学生的舞台。学生很自然地淘汰了一些较“麻烦”的方法，除个别学生仍选择用乘法列举求商，其余大部分选择用竖式笔算，只是试商的水平有差异。这就是孩子真实自然的学习过程。在教学试商和检验时，刘老师总是让学生出主意，与孩子商量着进行，孩子每时每刻都在思考和反思。】

三、在具体情境中自然感悟计算方法

1、买腐乳。

师：买了香干后，我又被平江的另一特产吸引了。（出示腐乳图片）这是什么？

生：腐乳。

（课件出示：刘老师还有196元，要买39元一瓶的腐乳，可以买多少瓶？还剩多少钱？）

（师引导学生列出算式：196÷39）

师：不计算，先估一估,看看可以买几瓶，并说说你的方法。

生1：可以买4瓶。把每一瓶看成40元，4乘40等于160，没有超过196。

生2：可以买5瓶，39乘5就是195，还剩1元钱。

生1：我觉得也是5瓶。

师：哦，你改变答案了。说说看。

生1：我把39看成40，看大了，我也应该可以把196看大一点就是200，200应该有5个40。

师：发现错了就及时更正，好样的。要想知道5到底对不对，怎么办？

生：验算。（过程略）

师：送给大家一句话（板书：千金难买回头看。）希望大家在计算完后，回头看看，验算一下。这样可以保证计算的正确。

师：谢谢大家帮我算出了腐乳的价格。回到宾馆，我试了试香干和腐乳，味道好极了。咱们平江人们真能干，做出这么美味的食品。

（学生们顿时自豪起来，身体都坐直了很多呢！）

2、买书

师：接着，我开始看书。我看了一本数学绘本。（课件出示书的图片）

师：这本书的名字叫——

生：《世界上最帅的猪》

师：猪还有最帅的呀？（生笑）其实这是讲述多种数数方法的书。

（课件出示：每册7元；全套共36册；200元买一套够吗？）

生：不够，最少都要200多元。

师：最少要200多元，谁能说的更明白一点？

生：就算是30本，每本7元，30乘7等于210，所以不够。

师：实际上我用了不到200块钱，就买了一套，这是怎么回事呢？

（课件出示：当当网上书店促销： 全套180元，每册多少钱？）

生1：180除以7。

生：不对，是180除以36。

师：为什么呢？

生：因为求每本多少钱，要用总钱数180除以总本数。180元买36本，不是7本。

生：180除以7，变成求180元，7元一本可以买多少本了。

师：你读题很认真。在这里，“每本7元”是个多余信息。

师：180除以36等于多少呢？

 （学生安静地计算。）

师：谁最先算对？你是怎么算的。

生：我是想36乘5就是180，所以180除以36就等于5。

生：我是看几乘6，个位是0，发现只有5乘6等于30，个位是0。

生：我是把36看成30，180除以30应该商6，但是我想商一定大了，所以就改商5了。

师：把36看成30商就会大，谁明白他的意思？

生：因为除数越小，商越大。他把36看成了30，那么试的商肯定比正确的商大了。

师：那如果把除数看大一点，试的商就会比正确的商怎么样？

生：小。

师：很好。

师：看完了书，我就看上个月刚买的光盘。光盘中也有数学问题。请看。

（教师读题：一套光盘270元，45元一张，一套光盘有几张？）

（很快就有几个同学忍不住说出正确答案“6”。）

师：6张，对不对呢？请你演算一下。

生：对了，用45乘6正好是270。

师：同学们真不错，不仅能算对，速度也越来越快了。

四、和学生分享学习的收获

师：光盘上有这样一句话，在我们以后学习分数中会用到，与大家分享。

（课件出示：数起源于数，量起源于量。教师建议学生齐读。）

当学生觉得莫名其妙时，出示拼音让大家再读，

shù     shǔ liàng  liáng

数起源于数，量起源于量。

（生开心地笑了。）

师：大家今天表现得非常好，我买了一套数学绘本送给大家，希望你们能爱上数学。

（学生嘴里纷纷叫着：世界上最帅的猪！下课了，有几个孩子张开手，希望老师拥抱她们，孩子们久久不愿离开教室……）

【点评：练习设计少而精，仍然沿用前面的思路：结合情境感悟除法计算，先估后算，学会自我调整与反思。】

【总评】

刘友华老师这堂数学课，让我有点不太敢相信这是一群革命老区的孩子——这么活泼自信、思维丰富、聪明睿智、敢于表达的孩子，和大都市的小学生比起来，丝毫也不逊色！是什么激发了他们的智慧与潜力、让他们全身心地投入到这节课当中来、成就了这堂精彩的计算课呢？

1、巧妙的情景创设。

刘老师设计的一系列情景串，巧妙而完整，让孩子觉得每做一个题都是必须的、有价值的，特别当老师需要学生的帮助时，孩子们就更加感到“义不容辞”了。刘老师适当地向孩子寻求帮助，满足了孩子们“被需要”的情感需求，恰好好处地调动学生的积极性；结合具体情境进行计算，有助于学生理解算理，枯燥的学习也显得充满了温情和趣味。

2、尊重孩子的教学设计。

对于学生来讲，把除数看做整十数来试商是一个学习的难点，需要学生估计、口算、反思、调整等综合性思维。因此很多老师教学这个内容时，更多地是想怎样把算法讲清楚、让学生全部掌握。可刘友华老师不一样，她首先考虑的是：孩子们会怎么想、怎么做？只有了解了学生的认知起点，才能顺应着孩子的思维进行教学设计。

因此，她先期给孩子做了一些前测，从中获得了一些启示。比如，她发现学生在做计算题时，习惯按程序进行计算，不太关注算理。但是当老师进一步追问时，学生就会有很多丰富的手段来说理和解释，这说明学生头脑中本来是有多样的算法的，如果老师能关注这些算法，学生就会把它们贡献出来，从而帮助大家更好地理解算理。比如课堂中有个学生用乘法一步步尝试去找到商，就是一种很真实、很朴素的想法，这种原始的方法能帮助学生更好地理解除法的意义，感知乘除法的关系；理解了意义，就能更好地掌握方法。

如果是老师单一的讲解，肯定不会有学生这样丰富，因为在我们老师眼里，只有书上的那个竖式才是教学的重点，我们只想让孩子快点掌握书上的最优方法，至于学习的原点和起点在哪，我们也许早已经忽视和淡忘了。而学生自己的方法呢，实际上每一种都是有价值的，首先它都是孩子自己思考的结果，其次这中间也蕴含了很丰富的策略，如：实物操作——这就是一种直观化手段；一步步想乘法求商——这是一种尝试列举的策略；看成以前学过的除数是整十数的除法——常用的转化策略；画线段图——典型的画图解决问题，等等。孩子的这些方法，虽然看起来有点儿稚嫩、有点儿笨拙，但是我们有没有想过：从孩子的思维起点出发，从最笨的方法开始，这种“慢”的学习过程，才是孩子自己真正意义上的学习！

3、足够的耐心与爱心。

刘老师与孩子仅仅相处四十分钟，可下课后孩子们仍然围着刘老师久久不愿散去，这是为什么？我想，是因为孩子们感到了刘老师对他们的爱和尊重。课堂里，一个学生用乘法列举的方式求商，可是仅列举到21×4=84、21×5=105、21×6=126，离正确答案还差两步。面对这样的孩子，刘老师没有失去耐心，她读懂了学生，安静地等待，让孩子自己完成剩下的两步。而这个孩子在前面的交流过程中也受到了启发，直接“跳”一步完成了任务，获得了全场一片掌声。类似这样的情况，课堂里多次出现。这些点点滴滴的细节，使这群孩子在短时间内，爱上了陌生的刘老师。

4、显著的教学效果。

今天的课堂轻松有趣，但是练习量并不大，那知识技能的目标达成如何呢？学生能正确的计算吗？带着这个问题，我们做了一个后测。后测题目共三个：

69÷23，90÷28，272÷42。

题目出示后，学生不是像前测那样见题就动笔，而是问：可以不写竖式吗？老师回答：可以，只要算对。在三分钟内，54名学生基本完成。结果如下：

69÷23——正确率100%；

90÷28——正确率96.3%（两人出错；见图一、图二)；

272÷42——正确率94.4%（三人出错，见图三、图四、图五）。

图一            图二              图三             图四            图五

出错的5人中，竖式中的商全部正确。1人是横式上的商出错；1人是商和除数相乘出错；3人是最后的相减错误。这说明，学生对于试商是掌握得好的。

实践表明：这节除法计算课，老师让学生先估后算，让学生展示各种试商方法，自己构建合适的、喜欢的试商方法，让学生在具体的情境中去解决除法问题，哪怕教师不教一种试商方法，学生也能很好地掌握；结合具体情境去计算，去检验，还能更好地帮助学生理解除法的算理，提高除法计算的正确率、提高学生发现错误、自我反思的能力。这是一次有价值的尝试，它使计算课散发出了魅力，让计算教学变得美妙！